4603. К-реберный граф
Дан ациклический ориентированный
граф из n вершин и k рёбер. Найти количество рёбер в его
транзитивном замыкании.
Транзитивное замыкание графа G –
граф G', состоящий из множества вершин исходного графа G и множества ребер (u,
v) таких, что существует путь из вершины u в вершину v в графе G.
Кнут знает, как решать эту задачу.
А Вы?
Вход. В первой строке два числа n и k (1 ≤ n, k
≤ 50000). В каждой из следующих k
строк находится по два целых числа ai
и bi, означающих наличие
ребра, ведущего из вершины ai
в bi (1 ≤ ai, bi ≤ n).
Граф не содержит петель, циклов и кратных рёбер.
Выход. Вывести
количество рёбер в транзитивном замыкании.
|
Пример
входа |
Пример
выхода |
|
5 6 1 2 2 3 3 5 4 5 1 5 1 3 |
7 |
РЕШЕНИЕ
графы –
маски
Анализ алгоритма
Маской
подмножества вершин графа будем называть последовательность из 0 и 1 длины |V|.
Маски будем хранить в целочисленном массиве (или структуре bitset). Запустим
поиск в глубину на входном ориентированном графе. В каждой вершине v будем строить подмножество вершин,
достижимых из v (не включая саму v). Если m1, …, mk
– маски сыновей v1, …, vk (в дереве поиска в
глубину) вершины v, то маска вершины v имеет вид:
m1 or … or mk
or 2v1 or … or
2vk
Количество ребер
в транзитивном замыкании, исходящих из вершины v, равно количеству единиц в битовой маске, соответствующей v.
Пример
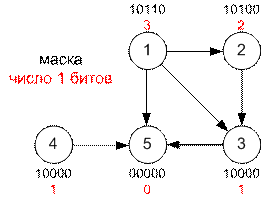
Младший бит в
маске соответствует вершине номер 1. Суммарное количество бит во всех масках
равно 3 + 2 + 1 + 1 + 0 = 7, что равно количеству ребер в транзитивном
замыкании.
Реализация алгоритма
Матрицу
смежности графа храним в массиве g. При поиске в глубину используем массив
пройденных вершин used. Массив mask[i]
хранит битовую маску вершин, в которые из i
имеется путь. bits[i] содержит количество бит в двоичном
представлении числа i.
#define MAX 50100
vector
<vector<int> > g;
int used[MAX], mask[MAX][MAX/32],
bits[1<<16];
Поиск в глубину из вершины v.
void dfs(int
v)
{
int i, j, to;
used[v] = 1;
for(i = 0; i
< g[v].size(); i++)
{
to = g[v][i];
if(!used[to])
dfs(to);
Для каждого сына to вершины v совершаем
операцию mask[v] = mask[v] OR mask[to].
for(j = 0;
j < MaskLen; j++) mask[v][j] |= mask[to][j];
Добавим в маску вершины v вершину to.
mask[v][to >> 5]|= 1 << (to
& 31);
}
}
Препроцессинг
массива bits. Ячейка bits[i] содержит
количество единиц в бинарном представлении числа i.
int gen(int
mask)
{
int i;
if (!mask) return 0;
if
(bits[mask]) return bits[mask];
for(i = 0; i
< 32; i++)
if (mask
& (1 << i)) bits[mask] = gen(mask ^ (1 << i)) + 1;
return
bits[mask];
}
Основная часть программы. Читаем
входные данные.
memset(bits,0,sizeof(bits));
gen((1 <<
16) - 1);
scanf("%d %d",&n,&k);
g.resize(n);
while(k--)
{
scanf("%d
%d",&i,&j);
g[i-1].push_back(j-1);
}
В ячейке типа int содержится 32 бита,
граф содержит n вершин. Для хранения
маски длины n бит достаточно использовать целочисленный массив длины MaskLen = ![]() .
.
MaskLen = (n +
31) / 32;
Запускаем поиск в глубину, в котором
строятся маски достижимости для каждой вершины.
for(i = 0; i < n; i++)
if(!used[i])
dfs(i);
Остается подсчитать количество единиц
во всех масках mask[i] (0 ≤ i ≤ n – 1).
for(res = 0, i = 0; i < n; i++)
for(j = 0; j
< MaskLen ; j++)
res += bits[mask[i][j] & 65535] +
bits[(mask[i][j]
>> 16) & 65535];
Выводим количество ребер в
транзитивном замыкании графа.
printf("%d\n", res);
Реализация при помощи bitset
#pragma comment
(linker, "/STACK:100000000")
#include <cstdio>
#include <vector>
#include <bitset>
#define MAX 50100
using namespace
std;
vector
<vector<int> > g;
int used[MAX];
int res, n, k, MaskLen;
bitset<MAX>
mask[MAX];
void dfs(int
v)
{
int i, j, to;
used[v] = 1;
for(i = 0; i
< g[v].size(); i++)
{
to = g[v][i];
if(!used[to])
dfs(to);
mask[v] |= mask[to];
mask[v].set(to);
}
}
int main(void)
{
int i, j, r;
scanf("%d
%d",&n,&k);
g.resize(n+1);
while(k--)
{
scanf("%d
%d",&i,&j);
g[i].push_back(j);
}
for(res = 0,
i = 1; i <= n; i++)
{
if(!used[i]) dfs(i);
res += mask[i].count();
}
printf("%d\n",
res);
return 0;
}